Geometric Proof

Squiffy  19 October 2013 11:14:54

Geometric Proof

The other day I was discussing a particular algorithm with a developer and I happened to mention that there was a Geometric Proof that demonstrated the correctness of a part of the algorithm. I was met with a blank stare and the question "What is a Geometric Proof?". I cast around for a simple example of a Geometric Proof and that was when I remembered how captivated I had been by the simplicity and elegance of the proof by geometric rearrangement for the Pythagoras theorem.

We are seeking to prove

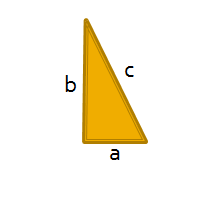For any right angled triangle show that the square of the hypotenuse (side opposite the right angle) is equal to the sum of the squares of the two other (adjacent) sides.


i.e. a² + b² = c².

Step 1

Take a square with sides a + b and place four of the triangles in the square in the following arrangement.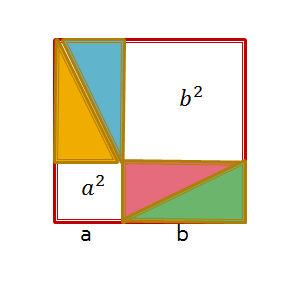



This arrangement already shows us something useful

(a + b)² = a² + b² + 2ab

Step 2

Re-arrange the four triangles in the square in the following pattern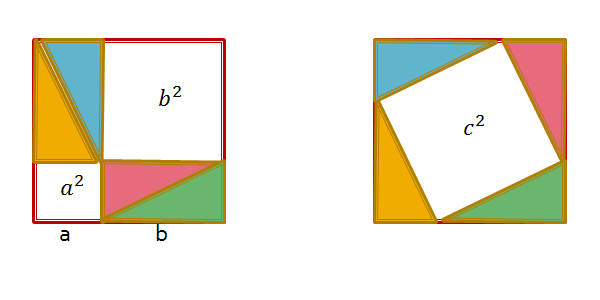



a² + b² + 2ab = c² + 2ab

Therefore a² + b² = c²    ......... Q.E.D.

The developer was suitably awed by this, now if only I could stop him producing a doodle "Geometric Proof" along with every piece of algorithm design he does then everything would be perfect!

Share:

Follow @SquiffyTheAAI

Tweet

• Comments [0]